１月の新聞では、大学の共通試験や有名高校の入学試験の問題と解答で紙面を占める日があります。その分読む記事は少なくなり、高校入試ならいけるかもと、一つ解いてみようとの気になりました。
問題は洛南高校（？、確かそうだったと思います）の幾何の問題です。
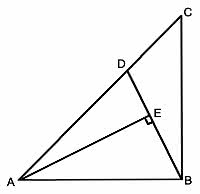ＡＢＣは一辺５cmの直角二等辺三角形で、Ｄは斜辺ＡＣを２：１に分割した点です。Ａより線分ＤＢに下ろした垂線との交点をＥとすると、三角形ＡＢＥの面積はいくらになるでしょう。
ＤＥ：ＥＢの比が求まれば簡単といろいろ考えますが、一向に解決策が見つかりません。仕事中も頭の隅に残ったままです。夕方になって、これは以前取り上げた折り紙による３等分問題と一緒だと気付きます。ＤはＡＢを一辺とする正方形の３分の１の点ですから。
思いつけば後は簡単、答は簡単に見つかりました。何事も行き詰まった時には、考え方の転換が必要です。ところが一度はまると、ともすればなかなか脱却できません。
解けるには解けましたが、制限時間をはるかにオーバーで、私の場合入学試験は不合格です。
