割り算の余りを材料に解く問題、例えば「5で割れば2残り、3で割れば1残る数は何~んだ?」というのはよくありますよね。一般的にどう解くのかなと調べていると、今の時代なんだって見つかります。
こう解くのだそうです。
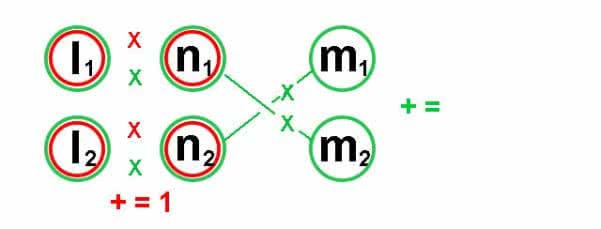
図で、ある数をn1で割ったときの余りがm1、n2で割ったときの余りがm2とすると、まず図の赤丸の積の和:l1xn1+l2xn2が =1 になる l1とl2を見つけます(試行錯誤ですね)。
それが見つかると求める答の数字は、図の緑丸の積の和:l1xn1xm2+l2xn2xm1 になるとのこと(但し答がマイナスだったり条件の範囲に入らなければ、割る数の最小公倍数を+ーする)。
最初の問題で考えてみると、l1=2、l2=-3 で赤丸の積の和が 1 になりますので、緑丸の積の和を求めると、
2x5x1+(ー3)x3x2=-8
答がマイナスですので、5と3の最小公倍数15を+すれば 7。確かにこれは問題にマッチします。数字が三つになると、まず二つで今のように答を見つけそれに最小公倍数を+-しながら三つ目の数の条件にあうかどうかで答を導くそうです。
せっかくの解き方ですが、以前紹介した「105減算」を知る者にとっては、その解き方の方が便利じゃないかと思います。日本独自の「和算」、胸を張れます。
