先日出かけた図書館で、大野栄一著『図形がおもしろくなる』を借りてきました。そこに折り紙で作る分度器の話があり、なるほど90度、45度、60度は簡単に折れるので、15度刻みの分度器は簡単にできます。
そこで更に、10度や5度刻みはどうかと考えると、どうしても角度の三等分が必要で、折り紙なら角度の三分の一が出せることを思い出し、ネットで見てみるとたくさんの記事がありました。ところがその証明となると、折り紙による角の三等分について(※1)などは、あまりに学術的で分りづらく自分で考えてみたくなり、解けたら解けたで書いてみたくなる私の悪い性分が頭をもたげます。悪いですがお付き合いください。
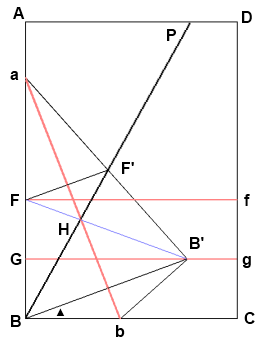
折りかたは他のサイトが詳しいですが簡単に説明しますと、長方形ABCDで対象となるを角PBC(鋭角でBに頂点)とします。辺BCと平行に適当に等間隔で折り線GgとFfをつけます。Bを持ち上げて線Gg上を移動しながらFが丁度PB上に来る位置で折り目(ab)を入れます。すると∠B’BC(図の▲)は∠PBCの三分の一になります。
さて証明ですが、GgとBCは平行ですから、∠GB’B=∠B’BC=▲、 B’は線分FBの垂直二等分線上にありますから、△FB’Bは二等辺三角形で、∠FB’G=∠GB’B=▲、
ところでFとF’、BとB’は線分abに対して線対称ですから、FF’とBB’は平行。かつFB=F’B’ですから、台形FF’B’Bは等脚台形です。したがって△FF’B’≡△FF’B(証明は省略します)で同じ△FF’Hを取り除いた△FHBと△F’HB’も合同です。故に△HB’Bは二等辺三角形であり、∠HB’B=∠HBB’=2▲。よって▲は与えられた角の三分の一になります。(∠は文字化けしているかもしれませんが、角の数学記号としてお読みください。)
さて証明ですが、GgとBCは平行ですから、∠GB’B=∠B’BC=▲、 B’は線分FBの垂直二等分線上にありますから、△FB’Bは二等辺三角形で、∠FB’G=∠GB’B=▲、
ところでFとF’、BとB’は線分abに対して線対称ですから、FF’とBB’は平行。かつFB=F’B’ですから、台形FF’B’Bは等脚台形です。したがって△FF’B’≡△FF’B(証明は省略します)で同じ△FF’Hを取り除いた△FHBと△F’HB’も合同です。故に△HB’Bは二等辺三角形であり、∠HB’B=∠HBB’=2▲。よって▲は与えられた角の三分の一になります。(∠は文字化けしているかもしれませんが、角の数学記号としてお読みください。)
(※1) http://www.jssac.org/Editor/Suushiki/V11/No3/V11N3,4_112.pdf
