大失敗です
私共のサイトは常時SSLを目的に、レンタルサーバー会社とSSL契約をしていますが、サーバーや他の契約同様自動更新とばかりおもっていました。ところが昨日サイトを訪れると、証明書の期限切れでSSLサイトにしているため逆に「安全でない」注意表示が出ています。
昨日は日曜日、レンタルサーバー会社との連絡も取れず、月曜日の今朝はサポート電話もさぞ混み合うことでしょう。
会社のサイトを見ると更新案内は60日、30日前にメールで連絡するとありますが、おそらく契約時点のメールアドレスへの連絡だったのでしょう。あいにくそのメールサーバーは解約していますので、メールが届くはずがありません。
更新までしばらくかかりそうです。私共のサイトを訪れていただく方には、誠に申し訳ありません。サイトが悪用されているなどということは決してありませんので、その点はご安心ください。
4倍すれば・・・
何度か取り上げている NSA の月替わりパズル、昨年12月出題(※1)は解かれましたでしょうか。
| R | A | T | S | |||
| x | 4 | |||||
|
|
||||||
| S | T | A | R | |||
という覆面算です。
条件が限られますので簡単に解けるでしょうが、パズルファンの方であれば問題を見ただけで答えが分かったことでしょう。「4倍すれば数字の順序が反転する4桁の数字」だからです。でも私は2倍と3倍でこれまた数字が反転することを、初めて知りました。
4倍すれば順序が反転する数は、5桁でも10桁でも20桁でもどんな桁数にもあります。先ほどの答えの4桁の真ん中に桁数に合わせて9をどんどん追加するだけです(覆面算にはなりませんが)。ちょっとした話のネタにご記憶ください。
(※1) https://www.nsa.gov/news-features/puzzles-activities/puzzle-periodical/2016/puzzle-periodical-09.shtml
NHK、ちょっと変じゃないですか
高市総務相がNHK職員の受信料着服の事実をしばらく隠蔽したことに苦言を呈したようですが、大臣でなくとも、このところのNHKは何か変だと誰もが思っているのではないでしょうか。
事務所にFAXは必需品ですが、名簿業者のデータを元にスパムファックスがよく届くのが困りものです。少し前にNHKから二度希望もしないファクスが届きました。「NHK業務委託説明会のご案内」とのタイトルで内容は、NHK放送受信料の契約・収納業務委託説明会です。二度目のファックスは同じ内容ですが、なんと「ご好評につき」との捕捉が付きます。
職員自らが行うのではなく、国からの予算をこんなことに使うのかと思うと大いに不満を覚えます。NHKは自らのより良い映像を視聴者に見せることに力点を置いているというよりも、利益を上げることに注力しているとしか思えません。
法律の曖昧さをついて解釈をNHKが独自に行っているのも不満です。テレビといえば、放送電波を受け取るだけの機器の時代から、今はネットの動画、レンタルビデオ、家族撮影ビデオ、ゲームなど、用途は多彩でテレビ局電波以外の利用の方が多い家庭もあるやも知れません。
地上波からBS、さらにはネット配信へと受信料拡大を画策していますが、地上波は大上段の言い分があるとして、不公平を問うならBSはそろそろスクランブル化してはいかがでしょう。
大臣も噛みつくばかりでなく、先日のスマートフォン訴訟のように、法律そのものが古いのですから、立法府として根本的な見直しに着手すべきではないでしょうか。
反応
メリル・ストリープさんのゴールデン・グローブ賞授賞式でのスピーチに、トランプ次期アメリカ大統領が反応をしたことが話題になっていましたので、そのスピーチの訳文(※1)を読んでみました。
実に真っ当なスピーチだとの感想です。名指しは避けるものの人種差別的な発言を批判されていることに、トランプ氏は反応したのでしょう。
指導者たる人物の発言には賛否両論が付きものです。それに対しいちいち角を立てていては指導者としては務まりません。反論すべき処は反論すべきですが、それはあくまでも正論での反論であるべきで、相手を茶化すような対応では人柄自体が問われます。記者会見で記者の障害を真似るなどもっての他です。
今回のやり取り、私はストリープさんに1本です。
(※1) https://www.instapaper.com/read/844470922
小町算
暮れの掃除で見つかったブルーバックスからの、 0~9までの数字を一回だけ使って数式を満たす小町算の問題です。
| A | B | C | D | ||||
| ー | E | F | G | H | |||
|
|
|||||||
| 4 | 8 | ||||||
A~Hの数字は何でしょう。
解答解説は、ABーEF は1なので既に出ている4,8を除くと、70ー69,60-59,30-29,20-19 のどれかで、Bは0、Fは9 と決まります。すると、DーH は、5-7,3-5 のどちらかしかなく、GはCより5大きくなります。こうして、C-G は、1-6,2-7 のどちらかとなります。条件は絞られましたので、あとは残りを組み合わせると、条件を満たす答えがただ一つだけ
| 3 | 0 | 1 | 5 | ||||
| ー | 2 | 9 | 6 | 7 | |||
|
|
|||||||
| 4 | 8 | ||||||
とつくれます。
ところがこの解説には抜けがあって、答えはもう一つ見つかります。作者の誤りを見つけるのは楽しいものです。ただ一つではない、もう一つの答えを見つけてください。
初詣
新年仕事始そしてブログ始めです。
毎年我が家の新春行事は、元旦の大神神社への初詣です。自宅から往復約3kmを家族一同歩いてお参りします。今年は温かい上に良い天気、初詣日和です。参道に着いて驚きました。二の鳥居より上は一方通行、しかも一向に前に進めません。それもそのはず、拝殿前の広場に上がる階段前で、ロープを張って人数制限をしています。毎年お参りをしていますが、初めての経験です。
天気の良さに誘われこぞって初詣に訪れたのでしょう。神社仏閣は、「今年は春から縁起がいい~~~わい」と六方を踏んでいそうです。少しおこぼれも頂きたく、賽銭箱に近づけないながら賽銭を投げ入れ、今年のお願いをしてきました。
謹賀新年
明けましておめでとうございます

今年もよろしくお願いいたします
熊の色
昔子供の頃こんな問題を出されました。「ある熊は毎日自宅から南へ2km歩いて友達とおしゃべりし、そこから東へ2km歩いて別の友達とおしゃべりして、そこから北へ2km歩いて自宅に戻ります。この熊は何色でしょう?」
答えは「白」。理由は「こんな条件にあう場所は北極点だから、熊は北極熊で色は白」。
解けなかった私は、そんな場所は北極にもあるだろう、とへそを曲げていましたが、最近になって答えを見つけました。
第2地点から東へ2km歩くと再び第2地点に戻れる場所ならば良いわけで、同じ緯度で2kmで地球を一周できる地点がそこに当たります。北極点以外でも南極点の近くにもそんな場所がありますよね。鬼の首を取った気分ですが、南極に熊っていましたっけ?
いつも拙い文章と内容にお付き合いをいただきありがとうございます。今年は今日がブログ納め、どうぞ良いお年をお迎えください。
ごみ箱作り
ここ桜井市はゴミ有料で、指定のゴミ袋を購入する形で支払いをします。その45リットルゴミ袋がきっちり収まる適当なゴミ箱が無く、それならばと作ることにしました。袋内でゴミの収まりが良いように底板は円形を考えましたが、切り取りも厄介で、側板の作りも難しいですから、直線裁ちで円形に近い正八角形にすることにします。

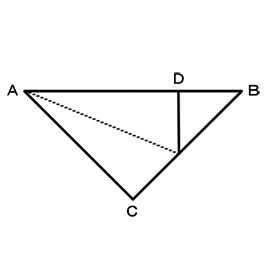
正方形各辺の切り取る位置は計算で求めることができますが、調べるとこれまた折り紙で簡単に求められることが分かりました。
元の正方形の実寸大の紙を三角形に二度折ると、左図の三角形ABCができます。角Aを二等分してCが線ABに重なるように折り重なった点をDとするとBDが求める長さになります。Dの位置に印を付け、角Bについても同じことをして印を付けて折った紙を元の正方形に広げると、四隅の切り欠き位置があらわれます。
もう一つ調べる過程で知ったのですが、この場合には「ルート2」という数字が関係してきます。大工さんが使う曲尺にはこのルート2倍した目盛りがあって、今回のBDの長さもその曲尺を使えば一瞬とのこと。先人の知恵はすばらしいです。
年末の片付け
新年に向けての片付け第二弾です。
気にはなっていたのですが、ついつい怠け心で何年も手を付けずにいた場所に、遂に重い腰をあげます。何から手を付ければいいものか。片付けは捨てること。ごっそりあるビデオテープをもう見る機器が無いし、デジタル化もお金と手間がかかるだろうと捨てることにします。昔、レンタルしたビデオがβではダビングできたので、懐かしいタイトルばかりですが、今となればネットで無料で見ることができたりして、なんと無駄なことをしてきたかとの感慨です。
次はこれまたごっそり出てきた撮りためた写真。さすがこれは捨てられません。どんな写真かなと片付けの手を止めバインダーを開くと、懐かしいやら、はたまたこれは何処での写真やら、「うわぁーこんな写真あったんや」と家人を巻き込み、次々開くアルバムでタイムスリップし懐かしさに浸ります。
時間の経つのは早いもの。ということで昨日の片付けはここまで。あとは来る祭日までおあずけです。
